I have come across some fun math problems (yes, math CAN be fun!) through the internet and friends. Here is a video of Japanese Multiplication. First watch the video, and then see if you can figure out how they are multiplying before you read my explanation below!
—————————————————————-
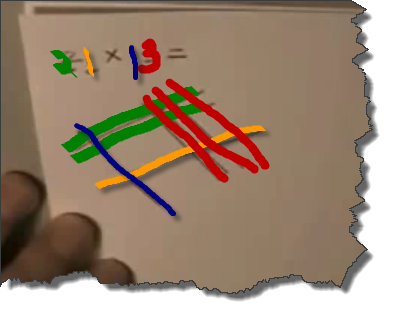
Well, did you figure it out? Let’s take a closer look at the first example:
Now take it apart:
- The first set of lines, the green ones in my image above, represent 2 sets of 10 , or 20
- The second region with one line, which is orange in my image, represents 1 set of 1
- Together these sets of lines, read top to bottom, represent 2×10 + 1×1 which is expanded notation for 21
Let’s look at the next set of lines that were drawn perpendicular to these lines:
- The first region that contains the 1 blue line represents 1 set of 10 or 1×10
- The second set of lines that were drawn, the three red lines, represent 3 sets of 1
- Together these 4 lines, read left to right, represent 1×10+3×1 = 13 in expanded notation.
Now for the tricky part!
Those of you who have ever FOIL-ed in Algebra will recognize the process of distributing the values by “First, Outer, Inner, Last”
Here is a quick Algebra example to remind you
(x+3)(2x+5) =
First = x * 2x = 2x^2
Outer= x*5 = 5x
Inner = 3*2x = 6x
Last = 3*5 = 15
Then, 2x^2 + 5x +6x +15 = 2x^2 + 11x +15 (the Outer and Inner were “like” terms, so could be added together)
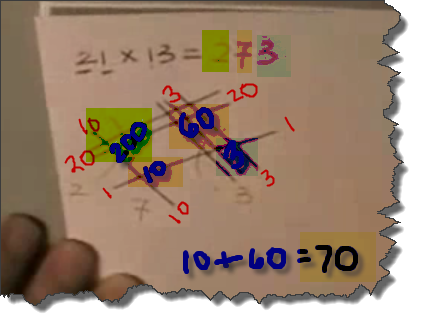
Now back to the arithmetic. If you look at the product 21×13 by separating out each factor by its place values, you have:
(20 + 1)(10 + 3) and now you can FOIL out the values, just like in the Algebra problem!
First = 20×10 = 200
Outer = 20×3 = 60
Inner = 1×10 = 10
Last = 1×3 = 3
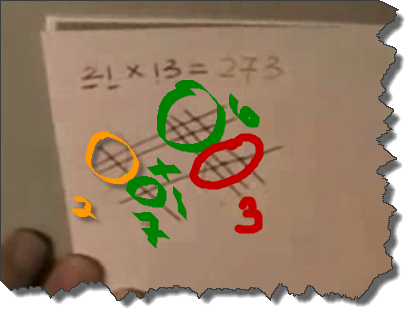
The 200 is represented by the 2 sets of crossing lines circled in yellow on the image above- that location on the paper represents the hundreds place value, so having a 2 in the hundreds location represents 2×100 = 200. In the video a 2 is placed as the first digit of the product, which will be the hundreds place.
Next:
The 60 is represented by the 6 sets of crossing lines in green on the top right
The 10 is represented by the 1 set of crossing lines in green on the bottom left
Together the 60+10 gives 70. In the video, the areas circled in green on the image above both represent the tens place value, so they are adding up the 6 crossed marks and the 1 crossed mark to get 7 sets in the tens place, or 7×10=70. They then place a 7 to the right of the 2 in the product (placing it in the tens place)
Finally:
The 3 is represented by the 3 crossed marks in the lower right (circled in red on the image above). This area of the paper represents the ones place, so we have 3×1 = 3. They then place a 3 to the right of the 7 in the product, placing the 3 in the ones place.
This gives the final product of 200+60+10+3 or 200+70+3 = 273
~Now look at the second product in the video and see if you can figure out how it works!
